How can you factor something like 6x^2+x-12?

To start, look for a common factor. There is none. 

You could use the ac method, but to do that you need to multiply 6 by -12 and then break that result down into factors — kind of feels like more work than you really should have to do. Is there a shortcut?

You need a pair of factors of ac. Those numbers are combinations of the factors of a and the factors of c. Instead of multiplying to create a big number, jump right into factoring: For a trinomial that looks like ax^2+bx+c, break a and c down into factor pairs. For 6x^2+x-12:

• a=6.  Factor pairs of a are 1,6 and 2,3.
• c=-12. Factor pairs of c are -1,12; 1, -12; -2,6; 2, -6; 3, -4; and -3,4.

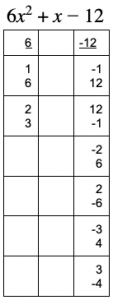
To find the magic numbers that we need so we can factor by grouping, we need to match the numbers up into two cross-column pairs. For example, if we use 1 for a (from the “6” column), we can match it with, say, -1 for c (from the “-12” column); once we do that, we need

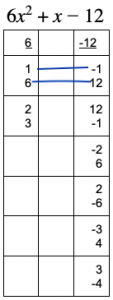to use the other term in the same box as 1 — that’s 6 — as well as the other c term in the same box as -1. That’s 12. Then one pair of possible magic numbers we could try would be 1*-1=-1 and 6*12=72. We need those numbers to add up to b, the multiplier of x in the middle term — in this case that’s 1.

Will -1 and 72 work as the pair of magic numbers we need? As stated above, the two magic numbers need to add up to 1. -1+72=71 is way off. We need two numbers whose absolute values are close together. 

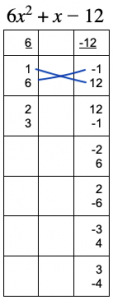Try 1 * 12 + 6 *-1 = 6. Getting closer, but there’s still a way to go. 

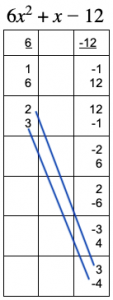Tr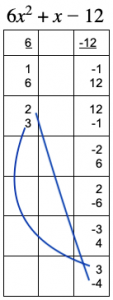y 2, 3 for a and 3, -4 for c? 2*3+3*-4=6 – 12 = -6. Doesn’t work, so try flipping the correspondence: 2*-4 +3 * 3 = -1. Bingo. The magic numbers are 2*-4=-8 and 3*3=9.

Now break up the middle term in accordance with the magic numbers you just found and factor by grouping:

6x^2+x-12

6x^2+9x-8x-12

Factor a common factor from the first two pairs and another common factor from the second two pairs:

3x(2x+3)-4(2x+3)

The contents of the parentheses are the same. Check. Now factor out 2x+3:

6x^2+x-12=(3x-4)(2x+3)

Let’s try another one, a really hard one. Factor:

20x^2-17x-63

What are the factor pairs of a and c?

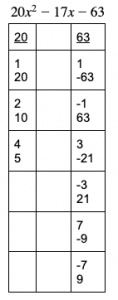
We need to match the numbers up into two cross-column pairs that add up to -17. 

Again, we can match up all possible pairs: 1*1 and 20 * -63 (=-1259, doesn’t work); 1 * -63 and 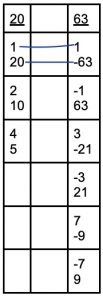 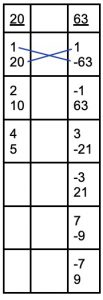20 *1 (=-43, doesn’t work) and work our way down the column that way. 

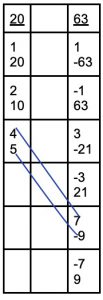With some trial and error*, you can find that the magic factor pairs are 4*7=28 and +5*-9=-45. 28-45=-17. Bingo.

20x^2-17x-63

Break that middle term up into two pieces whose coefficients are the magic numbers you just found: 28 and -45:

20x^2+28x-45x-63

Find a common factor in each pair of terms:

4x(5x+7) -9(5x+7)

The contents of the parentheses are the same. Check. Now factor out 5x+7. Then 20x^2-17x-63=(4x-9)(5x+7).

Multiply back and you’ll see that this is the correct factoring.

*There are ways to minimize that trial and error. That will be the topic of the next post.

Based on an idea from Math Lab tutor Yoel Abolnik.