Springs I

Elastic Springs

Purpose: To determine the stiffness of a spring

Objectives

To investigate how the stretching of an elastic spring is affected by the amount force applied to it.
To learn how to convert simple linear and mass units.
To learn how to compare the results from different runs for which you measure an experimental quantity.
To learn how to organize and interpret experimental data graphically.

Equipment

Springs, a hook, and weights
Meterstick
Mass Scales
Graph Paper

Theory

When a force is applied to an elastic spring, the amount it stretches is directly proportional to the amount of force applied and is given by Hooke’s Law:

Force = (stiffness) × (amount of stretching) (Eq. 1)

Note. It is important to note, that the direction of the force will always be opposite to what is happening to the spring. In other words, if the spring is being stretched, then the spring force will be pulling the spring back into its equilibrium. If it is being compressed, then the spring force will be pushing back to restore the spring into equilibrium.

When the spring stops moving and is in equilibrium, the elastic force must be counteracted by the gravitational force due to the weights (m×g). Thus, the elastic force can be calculated as:

Force = m × g

And we can re-write Eq.1 as:

m × g = (k) × (amount of stretching)

Note here (k) stands for the stiffness of the spring. Now the stiffness of the spring, k, will be:

(k) = (m × g) ⁄ (amount of stretching)

Experiment, Data and Results

Preliminary Setup

Hang a spring vertically. Set up a vertical rod clamped to the edge of the lab bench. Slide a clamp onto it, and hang the spring vertically onto the hook of the clamp.
Mark your zero! Place a meterstick vertically on the ground. Hang the hook to the lower end of the spring. Make sure the bottom of the hook is within the meterstick range.

Note on units and conversion. Make sure to convert all the masses and positions in kg and cm, as they must be consistent with the value for the gravitational acceleration 9.8 m/s².

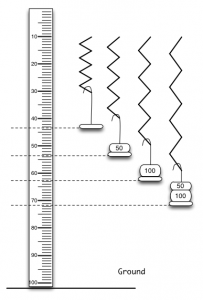
Activity:

Mark the bottom of the hook is along the vertical line – that is your “zero”. Write it down in meters!:

Hang a 50-g weight on the hook, wait for the spring to settle into its equilibrium state and record the vertical position of the bottom of the hook.

Repeat the system for 100-g, 150-g 200-g, and 250-g weights.

Write down your results in the following table. Note.The stretching of the spring will be the difference between the hook’s position with and without weights.

Questions.

Agree or Disagree? Compare your values of the spring stiffness. Look at their leading digits and see if they are the same. If all your results begin with the same first two digits, we will say that the results agree very well. If the results begin with the same first digit but disagree in the second, we will say that the results agree somewhat. And, if the results begin with different first digit, we will say that there is a disagreement.

Following the above guidelines, how do your results agree

Identify which run is the most suspicious and repeat it, and
List the factors that might have contributed to the “Disagree”-ing results:

Weights [kg]	Force [N]	Position [m]	Stretching [m]	Stiffness, k [N⁄m]
m	m ×g	y	Δy = y – y_o	k = (Δm × g) ⁄ (Δy)