Velocity and Acceleration

Motion With Constant Acceleration

Purpose

To determine the acceleration of an object sliding down a ramp.

Objectives

To learn how to use equipment for automated data acquisition.
To learn how to organize data.
To learn how to plot data and analyze it using statistical methods.
To learn how to determine physical quantities graphically.

Equipment

Air pump and air track with a glider
Spacers to incline the track, weights for the glider
A photogate to connect to Pasco 850 Interface
Ruler or calipers

Pre-lab Activity

Acceleration along a ramp.

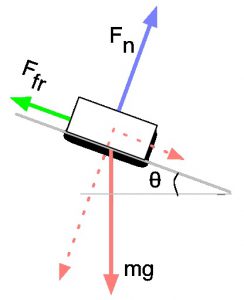When an object is sliding down an inclined ramp, several forces act upon it as shown on the diagram.

As the acceleration of the object is along the direction of the ramp, the forces, or the components of the forces acting perpendicularly to the ramp must add up to zero.

$F_n - mg \cos \theta = 0$

$mg \sin \theta - \mu F_n = ma$

Here, we have used the relation between the kinetic friction and the normal force, $F_{fr} = \mu F_n$ . Using the first equation to determine the normal force and plugging its value into the second equation, the acceleration of the object is:

$a = g \sin \theta - \mu g \cos \theta$

Question 1. You set up the slope the ramp is such as $\sin\Theta=0.2$ . Then, you measure the mass of the sliding object m = 400 g. Determine the acceleration in m/s² assuming the ramp is completely frictionless.

Question 2. After you perform the experiment, you measure the actual acceleration to be 1.4 m/s². Could this discrepancy be due to friction?

Question 3. Which statement below is correct?

The acceleration is:

The area under the velocity vs. time graph
The area under the velocity vs. position graph
The slope of the velocity vs. time graph
The slope of the velocity vs. position graph.

Theory

The acceleration of an object that slides along a frictionless incline is constant and in the absence of friction is is given by the formula

$a = g \sin \theta$ ,

where $g=9.8\;\text{m/s}^2$ is the gravitational acceleration, and $\theta$ is the angle between the track and the horizontal

Preliminary Setup

Turn on the air pump and level the track
Connect the photogate to the 850 Pasco Interface and set it up for “Photogate and Picket Fence“
Place a spacer under one of the track supports to incline it.
Check that the photogate blinks properly as the glider goes through it

Experimental and Measurements

Set the glider along the track above the photogate.
Turn on the air pump to level 3 and set the Pasco Software to record measurements
Let the glider move down the track through the photogate and stop the measurements.
Using the Pasco Software, graph the velocity vs. time measurements. Use linear fit to determine the least-square fit line and find its slope.
The slope of that graph is the acceleration of the glider.

Compare the theoretical prediction with your results for the acceleration

Use the theoretical formula and calculate the acceleration of an object sliding down an incline track
Compare the theoretical value with your experimental result

Question: What is the percent difference between the two values?

Analysis and Assignments

If you have a large discrepancy between the measured and the calculated acceleration work on A1. below. If your measured and calculated values for the acceleration agree to within 5% or less, work on A2. below.

A1. (Only if you have large discrepancy between the measured and calculated values for the acceleration). Check whether any of the following factors can be accountable for the discrepancy:

Check your calculations for the theoretical value of the acceleration.
Incorrect slope. Level the track again and re-rerun the experiment.
Photogate. Let the glider through the photogate and make sure the photogate blinks properly. There should be a blink (only one) for each blackened space along the picket fence.
Presence of friction. Increase the Air Pump level to 5 or higher and re-run the experiment.

Question: Which of the following factors affected your measurements?

Question: Were you able to obtain better results and improve the agreement between the experimental and theoretical value?

A2. (Only if your experimental and theoretical values for the acceleration agreed within 5%). Repeat the experiment for three more angles between the incline and the horizontal.

The theoretical acceleration is

$a = g \sin \theta = g \frac{h}{100}$ ,

where h is the height of the spacers used in cm, and 100 cm is the length along the incline between its two supports. Because of the geometrical configuration, $\sin \theta = \frac{h}{100}$ . Note that we don’t have to convert into meters, since we are working with dimensionless fraction.

Plot the acceleration $a$ as a function of the height of the spacers, $h$ , find the least-square fit line and its slope. Determine the gravitational acceleration from that slope.

Question: What is the agreement between your measurement for g and the established value of 9.8 m/s²