Vectors (online)

Addition and Subtraction of Vectors

Purpose

To add and subtract vectors graphically and by components.

Simulation Used

Vector Addition from the PhET at the University of Colorado

Objectives

To learn how to resolve vectors into components.
To learn how to add and subtract vectors by components.
To learn how to use vectors to calculate physics problems.

Theory

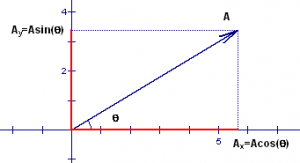
If we know the magnitude of the vector $\vec{A}$ and the angle it makes with the positive x-axis $\theta$ , its components are equal to:

A_x = A cos(θ) and A_y = A sin(θ)

Conversely, if we know the components of a vector, then we can determine its magnitude and direction with respective to the positive x-axis.

$A=\sqrt{A_x^2+A_y^2}$ and $\theta = \arctan \frac{A_y}{A_x}$

If a vector $\vec{C}=\vec{A}\pm\vec{B}$ , then its components can be calculated as:

C_x = A_x ± B_x and C_y = A_y ± B_y

Preliminary Settings

Open the simulation Vector Addition.
Select “Show Grid” from the menu on the right.

Activity 1. Switch from component- to magnitude-angle representation of a vector

Calculate the magnitude and the angle with respect to the positive x-axis for the following vectors. Check with the simulation to confirm your result.

Vector	Magnitude	Magnitude
	Calculated	From Simulation
(25, 10)
(-10, 5)

Question: For the second vector, did you get the same angle as the simulation showed?

Activity 2. Adding and Subtracting Vectors

For the vectors $\vec{A}=(10,25)$ , $\vec{B}=(-3,7)$ , and $\vec{C}=(-4,-10)$ , calculate the components, the magnitude, and the direction of each vector given in the table.

	x-component	y-component	Magnitude	Angle
A + B
B - C

Question: Were your results confirmed by the simulation?

Activity 3. Solving a Problem

Oasis B is located 25 km east from oasis A. A camel starts from oasis A and travels 19.6 km in the direction 14.7 degrees south of east. Then it walks 8 km directly to the north. How far is the camel from oasis B?

Hint: Use the simulation to construct the path of the camel so that you can visualize the problem better.

Question: In which quadrant is the camel located after the second leg of the trip?

Results

Submit your results to receive credit for the lab.