AC Circuits*

Purpose

To investigate the voltage across the capacitor as a function of the frequency in an AC circuit of a resistor and capacitor connected in series.

Objectives

To calculate the impedance of a RC AC circuit
To learn the relation between the voltage across each element in an AC circuit of R and C element in series.
To find out the dependence of the voltage across the C element as a function of the frequency of the input signal

Simulation Used

University of Colorado PhET Circuit Construction Kit AC+DC Circuits.

Definitions

A capacitor in an AC circuit has capacitive reactance of:

$X_{C}=\frac{1}{\omega C} = \frac{1}{2\pi f C}$

An inductor in an AC circuit has inductive reactance of:

$X_{L} = \omega L = 2 \pi f L$

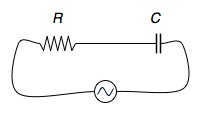
Activity 1. Low Pass Filter (RC-series)

Theory

We built a low-pass filter by connecting a resistor and capacitor in series. The impedance of the circuit is:

$Z = \sqrt{R^2+X_C^2}$

If the current in the circuit is given by $I=I_o \sin \omega t$ , the maximum voltage across is:

$V_o=ZI_o$

The maximum voltage across the capacitor is:

$V_{oC}=X_C I_o$

The ratio between the two then is given as:

$\frac{V_{oC}}{V_o} = \frac{X_C}{Z}=\frac{1}{2\pi f C \sqrt{R^2 + 4 \pi^2 f^2 C^2}}$

$\frac{V_{oC}}{V_o} = \frac{1}{\sqrt{4\pi^2 f^2 C^2 R^2+1}}$

When the frequency is zero the ratio is simply 1. When the frequency becomes very large ( $f \rightarrow \infty$ ), the limit of the ratio goes to zero. The cut-off frequency is that frequency for which the ratio is one half:

$\frac{1}{2}=\frac{1}{\sqrt{4\pi^2 f^2 C^2 R^2+1}} \rightarrow f = \frac{1}{2\pi RC}$

Settings

Open the PhET Circuit Construction Kit AC+DC Circuits simulation and construct an RC circuit with a 10-Ohm resistor, 0.05-F capacitor, and a 10.0-V AC source. Connect a Voltage Chart and a Voltmeter across the capacitor. Use the Voltage Chart to see how the voltage changes across the capacitor, and the voltmeter to determine its peak values.

Data and Results

Measure the maximum voltage across the capacitor and calculate the output ratio between it and the maximum voltage in the circuit (10.0 V) for each frequency given below:

Frequency (Hz)	V_C (V)	Output Ratio
0.1
0.2
0.3
0.4
0.5
0.6
0.7

In a spreadsheet, plot Output Ratio vs. F (Hz). Does the cutoff frequency from the graph agree with the theoretical value?

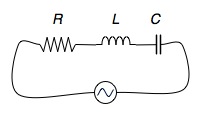
Activity 2. Impedance of RLC series circuit

Theory

When a resistor, inductor, and capacitor are connected in series to an AC source, the impedance of the circuit is:

$Z=\sqrt{R^2+\left(X_L-X_C\right)^2} = \sqrt{R^2+\left(2\pi f L - \frac{1}{2\pi f C}\right)^2}$ (Eq. 1)

The amplitude of the current in the circuit is given by:

$I_o = \frac{V_o}{Z}$ (Eq. 2)

and it is the largest when the impedance has the smallest value. The frequency at which the impedance is the smallest is:

$f = \frac{1}{2 \pi LC}$ (Eq. 3)

If the current through and the voltage across the resistor are given by

$I_R=I_o \sin (2\pi f t)$

$V_R=V_o \sin (2\pi f t)$

then the voltage across the inductor will be (leading ahead of the value for the electric current by π/2):

$V_L=V_o \sin (2\pi f t + \pi /2)$

and the voltage across the capacitor will be (lagging behind the value of the electric current by π/2):

$V_C=V_o \sin (2\pi f t-\pi/2)$

In the RLC circuit, the total voltage will be the sum of the voltage across all three elements:

$V=V_o \sin (2\pi f t + \phi)$ (Eq. 4)

Here φ is the phase difference between the electric current through and the total voltage across the RLC circuit and theoretically it must be equal to:

$\tan \phi = \frac{X_L-X_C}{R}$ (Eq. 5)

Experimentally, φ can be found by measuring the value for the voltage across the circuit when the current through is zero. Then $2 \pi f t = 0$ and Eq. 4 becomes:

$V = V_o \sin \phi$ (Eq. 6)

Settings

Open the simulation and connect a 10-Ω resistor, 10-H inductor, and a 0.1-F capacitor in series with an AC source of 10.0 V amplitude and frequency of 0.5 Hz.
For the given values, calculate the impedance of the circuit and the phase difference between the current and the voltage in the circuit using Eqs. (1) and (5). These are the theoretical values.
Place an ammeter in series with the RLC elements the measure the current in the circuit. Place a Voltage chart and a Voltmeter across the RLC portion to measure the voltage across.

Data and Results

Measure the maximum values for the current through and the voltage across the circuit. You might stop the simulation and progress step by step to find the maximum values from the ammeter and the voltmeter.
The experimental value for the impedance is calculate by using Eq. 2
When the current through the circuit is zero, determine the voltage across the circuit, V. Calculate the phase difference by using Eq. 6: $\sin \phi = \arcsin \frac{V}{V_o}$

Data Table

Record your data in a table where you compare the theoretical with the experimental values:

R (Ω)	L (H)	C (F)	f (Hz)
10	10	0.1	0.5
Z_theor	Z_exp	φ_theor	φ_exp

Results

Post the results from Activity 1 and 2 electronically on BB.